Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
To find least common multiple by using prime factorization method is discussed here.
To find the LCM of two or more numbers, we first find all
the prime factors of the given numbers and write them one below the other. Take
one factor from each common group of factors and find their product. Multiply
the product with other ungrouped factors. The resultant is the LCM of given
numbers.
Step I: Resolve each given number into its prime factors and express the factors obtained in exponent form.
Step II: Find the product of the highest powers of all the factors that occur in any of the given numbers.
Step III: The product obtained in Step II is the required least common multiple (L.C.M).
For example:
1. Find the least common multiple (L.C.M) of 9 and 15 by using prime factorization method.
Solution:
Step I:
Resolving each given number into its prime factors.

9 = 3 × 3 = 3².
15 = 3 × 5.
Step II:
The product of all the factors with highest powers.
= 3^2 × 5 = 3 × 3 × 5 = 45.
Step III:
The required least common multiple (L.C.M) of 9 and 15 = 45.
2. What is the least common multiple (L.C.M) of 16 and 28 by using prime factorization method?
Solution:
Step I:
Resolving each given number into its prime factors.

16 = 2 × 2 × 2 × 2 = 24.
28 = 2 × 2 × 7 = 22 × 7.
Step II:
The product of all the factors with highest powers.
= 24 × 7 = 2 × 2 × 2 × 2 ×7 = 112.
Step III:
The required least common multiple (L.C.M) of 16 and 28 = 112.
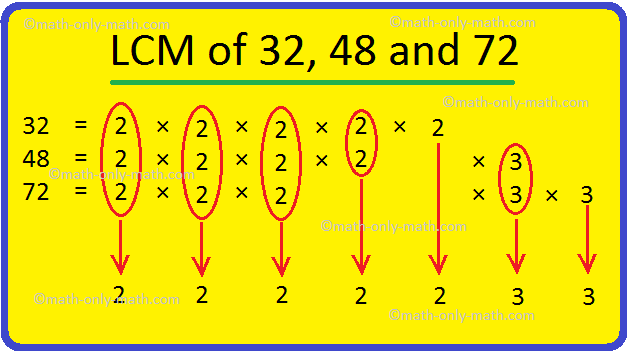
3. Find the LCM of 32, 48 and 72 by prime factorization.
Solution:
LCM of 32, 48 and 72 = 2 × 2 × 2 × 2 × 2 × 3 × 3 = 288.
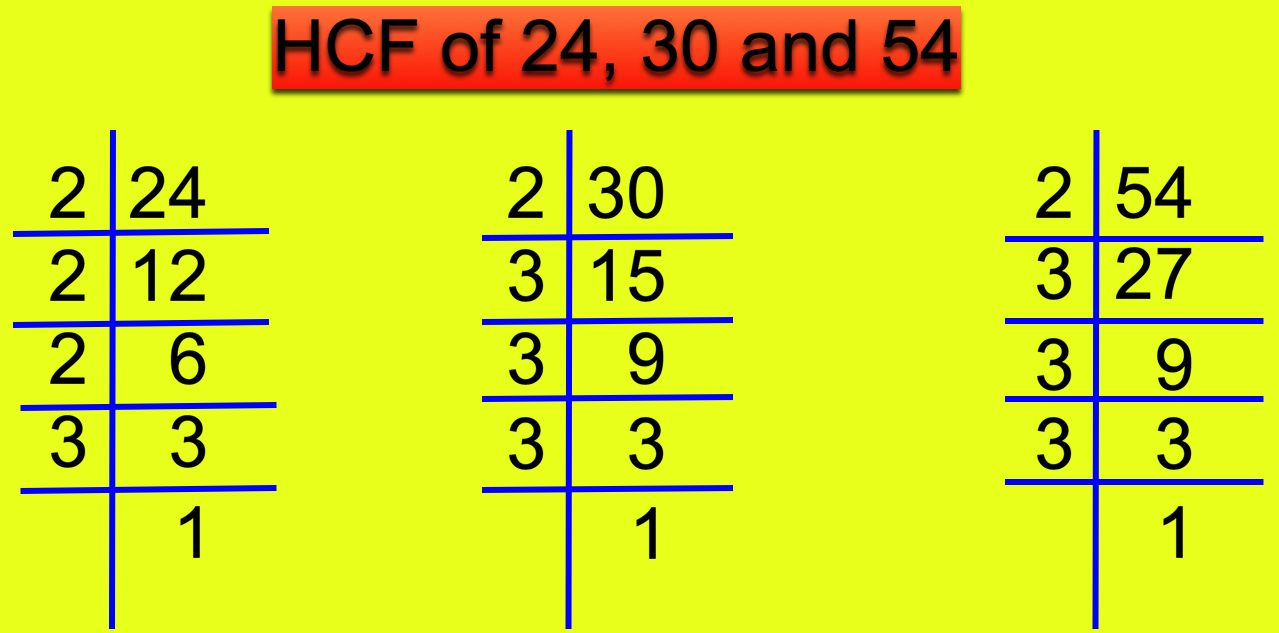
4. Find the LCM of 24, 30 ans 54 by prime factorisation method.
Solution:
First, find the prime factors of each number.
The prime factors of 24 = 2 × 2 × 2 × 3
The prime factors of 30 = 2 × 3 × 5
The prime factors of 54 = 2 × 3 × 3 × 3
From the above, we observe that 2 occurs as a prime factor maximum three times, 3 occurs as a prime factors maximum three times and 5 occurs only once.
Hence, the required LCM is 2 × 2 × 2 × 3 × 3 × 3 × 5 = 1080.
5. Find the LCM of 60, 70 ans 108 by prime factorisation method.
Solution:
First, find the prime factors of each number.
The prime factors of 60 = 2 × 2 × 3 × 5
The prime factors of 70 = 2 × 5 × 7
The prime factors of 108 = 2 × 2 × 3 × 3 × 3
From the above, we observe that 2 occurs as a prime factor maximum two times, 3 occurs as a prime factors maximum three times and 5 and 7 occur only once.
Hence, the required LCM is 2 × 2 × 3 × 3 × 3 × 5 × 7 = 3780.
Least Common Multiple (L.C.M).
To find Least Common Multiple by using Prime Factorization Method.
Examples to find Least Common Multiple by using Prime Factorization Method.
To Find Lowest Common Multiple by using Division Method
Examples to find Least Common Multiple of two numbers by using Division Method
Examples to find Least Common Multiple of three numbers by using Division Method
Relationship between H.C.F. and L.C.M.
Worksheet on H.C.F. and L.C.M.
Word problems on H.C.F. and L.C.M.
Worksheet on word problems on H.C.F. and L.C.M.
From To find Least Common Multiple by using Prime Factorization Method to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.