Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Worksheet on divisibility rules will help us to practice
different types of questions on test of divisibility by 2, 3, 4, 5, 6, 7, 8, 9,
10 and 11. We need to use the divisibility rules to find whether the given
number is divisible by 2, 3, 4, 5, 6, 7, 8, 9, 10 and 11.
A quick way to find factors of larger numbers is to perform
divisibility test. There are certain rules to check divisibility of numbers.
Divisibility by 2:
A number is divisible by 2, if the digit at ones place is an
even number, that is the number ends in 0, 2, 4 or 8. For example, 100, 222,
344, 1658 are divisible by 2.
Divisibility by 3:
A number is divisible by 3, if sum of all its digits is divisible by 3. Let us check if 27648 is divisible by 3. Sum of digits = 2 + 7 + 6 + 4 + 8 = 27; 27 ÷ 3 = 9. Hence 27648 is exactly divisible by 3.
Divisibility by 4:
A number is divisible by 4, if the number formed by its last 2 digits is divisible by 4. Let us check if 1124 is divisible by 4. Number formed by last 2 digits 24 is divisible by 4.
Divisibility by 5:
A number is divisible by 5, if it ends in 0 or 5. For example 100, 225, 605, 8000, 9925 are divisible by 5.
Divisibility by 9:
A number is divisible by 9, if sum of its digits is divisible by 9. Let us check if 16911 is divisible by 9.
Sum of digits = 1 + 6 + 9 + 1 + 1 = 18. It is exactly divisible by 9.
Divisibility by 10:
All numbers ending in 0 are divisible by 10. For example 8000, 9010, 11020, 98670 are divisible by 10.
1. Which of the following numbers are divisible by 2, 5 and 10?
(i) 149
(ii) 19400
(iii) 720345
(iv) 125370
(v) 3000000
2. Check whether the numbers are divisibility by 4:
(i) 23408
(ii) 100246
(iii) 34972
(iv) 150126
(v) 58724
(vi) 19000
(vii) 43938
(viii) 846336
3. In each of the following numbers without doing actual
division, determine whether the first number is divisible by the second number:
(i) 3409122; 6
(ii) 17218; 6
(iii) 11309634; 8
(iv) 515712; 8
(v) 3501804; 4
4. 6 is a factor of 12066 and 49320. Is 6 a factor of 49320
+ 12066 and 49320 – 12066?
5. Is 9 a factor of the following?
(i) 394683
(ii) 1872546
(iii) 5172354
6. Fill in the smallest digit to make the number divisible
by:
(i) by 5 : 7164__, 32197__
(ii) by 3 : 1__43, 47__05, __316
(iii) by 6 : __428, 9__52, 721__
(iv) by 4 : 2462__, 91__ __, 670__
(v) by 8 : 1232__, 59__16, 4642__
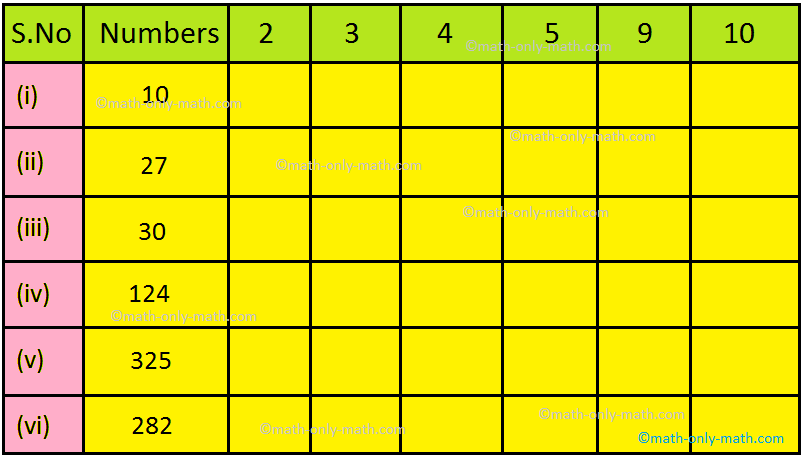
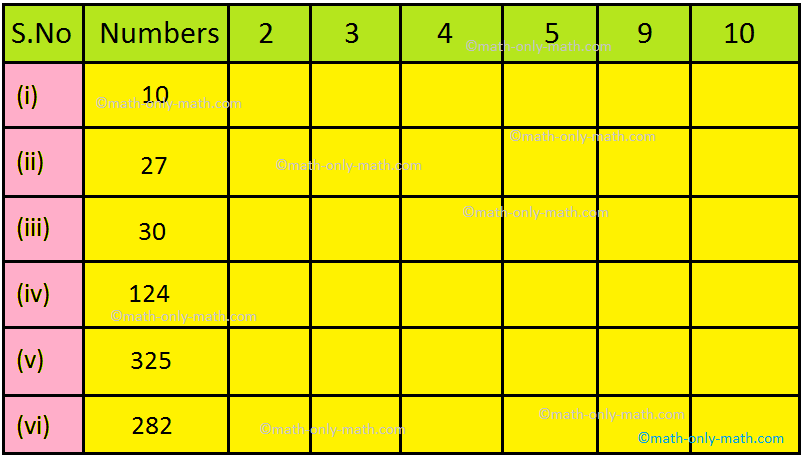
7. Using the divisibility rules check whether the number is divisible by the given numbers. Put P (tick) or û (cross).
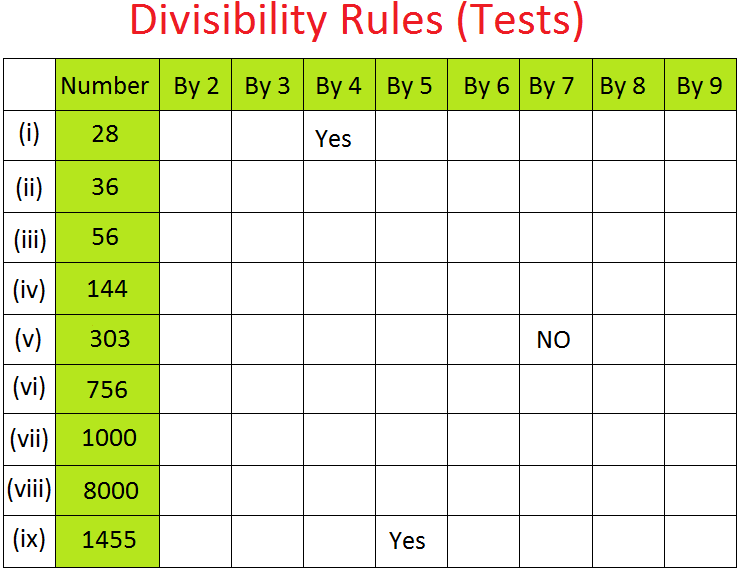
8. Check using divisibility rules and fill in the boxes using “Yes” or “No”.
9. Which of the two nearest numbers to 19506 are divisible by 9?
10. Choose the right answer:
(i) The number with unit digit 0 or 5 is divisible by:
(a) 2
(b) 3
(c) 4
(d) 5
(ii) The number with unit digit 0, 2, 4, 6 or 8 is divisible
by:
(a) 2
(b) 3
(c) 4
(d) 5
(iii) The number with unit digit 0 is divisible by:
(a) 5
(b) 10
(c) 15
(d) 2
(iv) 3681 is divisible by:
(a) 4
(b) 5
(c) 9
(d) 10
(v) 1170 is not divisible by:
(a) 10
(b) 9
(c) 5
(d) 4
(vi) Which of the following numbers is not divisible by 2?
(a) 1086
(b) 2869
(c) 3364
(d) 7000
(vii) Which of the following numbers is not divisible by 3?
(a) 1173
(b) 2391
(c) 3902
(d) 6048
(viii) Which of the
following numbers is not divisible by 4?
(a) 1084
(b) 3516
(c) 3328
(d) 7001
(ix) Which of the following numbers is not divisible by 10?
(a) 2015
(b) 3000
(c) 4170
(d) 8990
(x) Which of the following numbers is divisible by 9?
(a) 1284
(b) 3510
(c) 4328
(d) 7301
11. Multiple Choice Questions (MCQ) on Divisibility Rules:
Tick (✔) the correct option.
(i) Which of the following numbers is divisible by 2?
(a) 2508; (b) 2711; (c) 3915; (d) 409
(ii) Which of the following numbers is divisible by 6?
(a) 5024; (b) 7125; (c) 3018; (d) 7123
(iii) Which of the following numbers is divisible by both 5 and 10?
(a) 1055; (b) 2305; (c) 675200; (d) 3124
(iv) Which of the following numbers is divisible by 6?
(a) 60466176; (b) 59624565; (c) 45879632; (d) Both (a) and (b)
(v) Which of the following numbers is divisible by 11?
(a) 77585896; (b) 55505555; (c) 11440411; (d) 19487171
12. Check the divisibility of the following numbers by 4:
(i) 19536
(ii) 9862
(iii) 28037
(iv) 675083
13. Check the divisibility of the following numbers by 6:
(i) 59730
(ii) 18620
(iii) 83652
(iv) 32508
14. Check the divisibility of the following numbers by 9:
(i) 1098
(ii) 871245
(ⅲ) 257069
(iv) 125083
15. Check the divisibility of the following numbers by 8:
(i) 9408
(ii) 871245
(iii) 57896
16. Check the divisibility of the following numbers by 11:
(i) 61809
(ii) 70169803
(iii) 3178965
17. State True or false.
(i) If two numbers are divisible by a number, then their sum, difference and product are also divisible by that number.
(ii) The largest 4-digit number divisible by 11 is 9999.
(iii) Numbers not divisible by 2 are called even numbers.
18. Match the Columns:
|
Column A |
Column B |
|
(i) 2023 (ii) 24804 (iii) 12892 (iv) 6016 |
(a) divisible by 3 (b) divisible by 11 (c) divisible by 8 (d) divisible by 7 |
19. Test whether the following numbers are divisible by 2, 4 or 8:
(i) 268
(ii) 58258
(ⅲ) 65850
20. Test whether the following numbers are divisible by 5 or 10:
(i) 44125
(ii) 782381
(iii) 583320
21. Test whether the following numbers are divisible by 3 or 9:
(i) 8652
(ii) 47046
(iii) 90403
22. Test whether the following numbers are divisible by 11:
(i) 9867
(ii) 542367
(iii) 180301
(iv) 4932536
23. Test whether the following numbers are divisible by 6:
(i) 8459
(ii) 92376
(iii) 72846
(iv) 93672
24. Fill in the blanks with the smallest digit to make the number divisible by 3:
(i) 5 _ 860
(ii) 47 _ 93
(iii) 944 _ 4
(iv) 5 _ 7705
25. Fill in the blanks with the smallest digit to make the number divisible by 9:
(i) _ 9569
(ii) 74 _ 08
(iii) 276 _ 47
(iv) 2923 _ 1
26. Fill in the blanks with the smallest digit to make the number divisible by 11:
(i) 315 _ 5
(ii) 6338 _ 9
(iii) 33 _ 8231
(iv) 55 _ 5755
27. Find the largest number that you need to test as a divisor to determine whether each of the following is a prime number:
(i) 101
(ii) 111
(iii) 397
(iv) 401
(v) 487
(vi) 227
28. If a number is divisible by 2 and 7, will it be divisible by 14? Give an example.
29. If a number is divisible by 4 and 6, is it necessary that it will be divisible by 24? If not, write one such number.
30. Is 5720910 divisible by 7?
31. A number is divisible by both 6 and 11. By which other number will that number be always divisible?
32. A number is divisible by 45. By what other numbers will that number be divisible?
33. State True or False.
(i) If a number is divisible by 9, it must be divisible by 3.
(ii) If a number is divisible by 3 and 6, it is divisible by 18.
(iii) All numbers which are divisible by 2 must also be divisible by 4.
(iv) If a number exactly divides the sum of two numbers, it must exactly divides the two numbers separately.
Answers for the worksheet on divisibility rules are given below.
Answers:
1. (ii) 19400
(iv) 125370
(v) 3000000
2. (i) 23408
(iii) 34972
(v) 58724
(vi) 19000
(viii) 846336
3. (i) Yes
(ii) No
(iii) No
(iv) Yes
(v) Yes
4. Yes
5. (iii) 5172354
6. (i) 0, 0
(ii) 1, 2, 2
(iii) 1, 2, 2
(iv) 0, 00, 0
(v) 0, 0, 4
7. (i) P, û, û, P, û, P
(ii) û, P, û, û, P, û
(iii) P, P, û, P, û, P
(iv) P, û, P, û, û, û
(v) û, û, û, P, û, û
(vi) P, P, û, û, û, û
8. (i) Yes, No, Yes, No, No, Yes, No, No
(ii) Yes, Yes, Yes, No, Yes, No, No, Yes
(iii) Yes, No, Yes, No, No, Yes, Yes, No
(iv) Yes, Yes, Yes, No, Yes, No, Yes, Yes
(v) No, Yes, No, No, No, No, No, No
(vi) Yes, Yes, Yes, No, Yes, Yes, No, Yes
(vii) Yes, No, Yes, Yes, No, No, Yes, No
(viii) Yes, No, Yes, Yes, No, No, Yes, No
(ix) No, Yes, No, Yes, No, No, No, No
9. 19503, 19512
10. (i) (d) 5
(ii) (a) 2
(iii) (b) 10
(iv) (c) 9
(d) 10
(v) (d) 4
(vi) (b) 2869
(vii) (c) 3902
(viii) (d) 7001
(ix) (a) 2015
(x) (b) 3510
11. (i) (a) 2508
(ii) (c) 3018
(iii) (c) 675200
(iv) (a) 60466176
(v) (d) 19487171
12. (i) 19536 is divisible by 4
(ii) 9862 is not divisible by 4
(iii) 28037 is not divisible by 4
(iv) 675083 is not divisible by 4
13. (i) 59730 is divisible by 6
(ii) 18620 is not divisible by 6
(iii) 83652 is divisible by 6
(iv) 32508 is divisible by 6
14. (i) 1098 is divisible by 9
(ii) 871245 is divisible by 9
(ⅲ) 257069 is not divisible by 9
(iv) 125083 is not divisible by 9
15. (i) 9408 is divisible by 8
(ii) 871245 is not divisible by 8
(iii) 57896 is divisible by 8
16. (i) 61809 is divisible by 11
(ii) 70169803 is divisible by 11
(iii) 3178965 is not divisible by 11
17. (i) True
(ii) True
(iii) False
18. (i) → (d)
(ii) → (a)
(iii) → (b)
(iv) → (c)
19. (i) Divisible by 2 and 4.
(ii) Divisible by 2 and 4.
(ⅲ) Divisible by 2 only.
20. (i) Divisible by 5 only.
(ii) Neither divisible by 5 nor by 10.
(iii) Divisible by both 5 and 10.
21. (i) Divisible by 3 only.
(ii) Divisible by 3 only.
(iii) Neither divisible by 3 nor by 9.
22. (i) Yes
(ii) No
(iii) Yes
(iv) No
23. (i) No
(ii) Yes
(iii) Yes
(iv) Yes
24. (i) 2
(ii) 1
(iii) 0
(iv) 0
25. (i) 7
(ii) 8
(iii) 1
(iv) 1
26. (i) 1
(ii) 0
(iii) 8
(iv) 9
27. (i) 11, Yes
(ii) No
(iii) 19, Yes
(iv) 23, Yes
(v) 23, Yes
(vi) 17, Yes
28. Yes, 28
29. No, 36
30. No
31. 66
32. 1, 3, 5, 9, 15 and 45
33. State True or False.
(i) True
(ii) False
(iii) False
(iv) False
Problems on Divisibility Rules
Worksheet on Divisibility Rules
From Worksheet on Divisibility Rules to HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.